-

Reducing Reparameterization Gradient Variance
23 May 2017
Nick Foti, Alex D’Amour, Ryan Adams, and I just arxiv’d a paper that focuses on reducing the variance of the reparameterization gradient estimator (RGE) often used in the context of black-box variational inference. I’ll give a high level summary here, but I encourage you to check out the paper and the code.
(expand) -
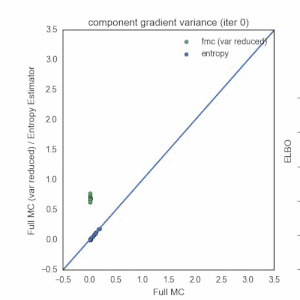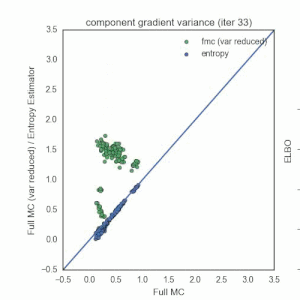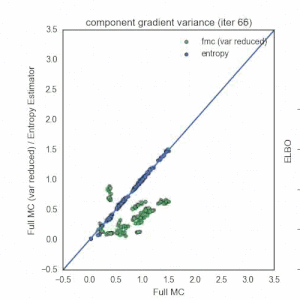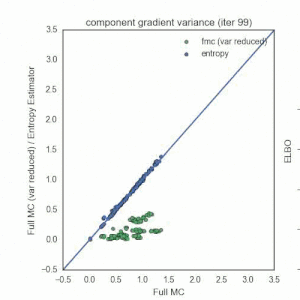
Monte Carlo Gradient Estimators and Variational Inference
19 December 2016
First, I’d like to say that I thoroughly enjoyed the the Advances in Approximate Bayesian Inference workshop at NIPS 2016 — great job Dustin Tran et al. An awesome poster (with a memorable name) from Geoffrey Roeder, Yuhuai Wu, and David Duvenaud probed an important, but typically undiscussed choice that practitioners have to make when doing black-box variational inference with the pathwise gradient estimators[^vi]. This post describes the phenomenon that they point out. I will try to provide some additional intuition through wordy prose and a numerical experiment on a simple example.
(expand) -
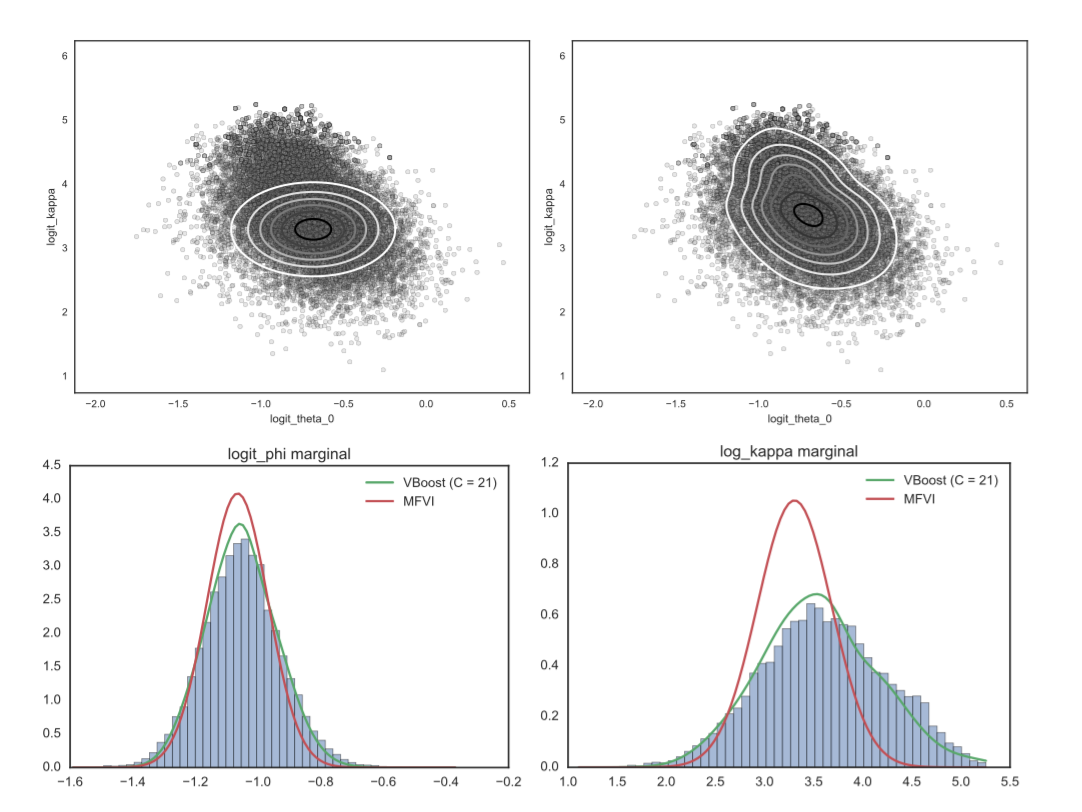
Improving Variational Approximations
23 November 2016
Nick Foti, Ryan Adams, and I just put a paper on the arxiv about improving variational approximations (short version accepted early to AABI2016). We focused on one problematic aspect of variational inference in practice — that once the optimization problem is solved, the approximation is set and there isn’t a straightforward way to improve it, even when we can afford some extra compute time.
(expand) -
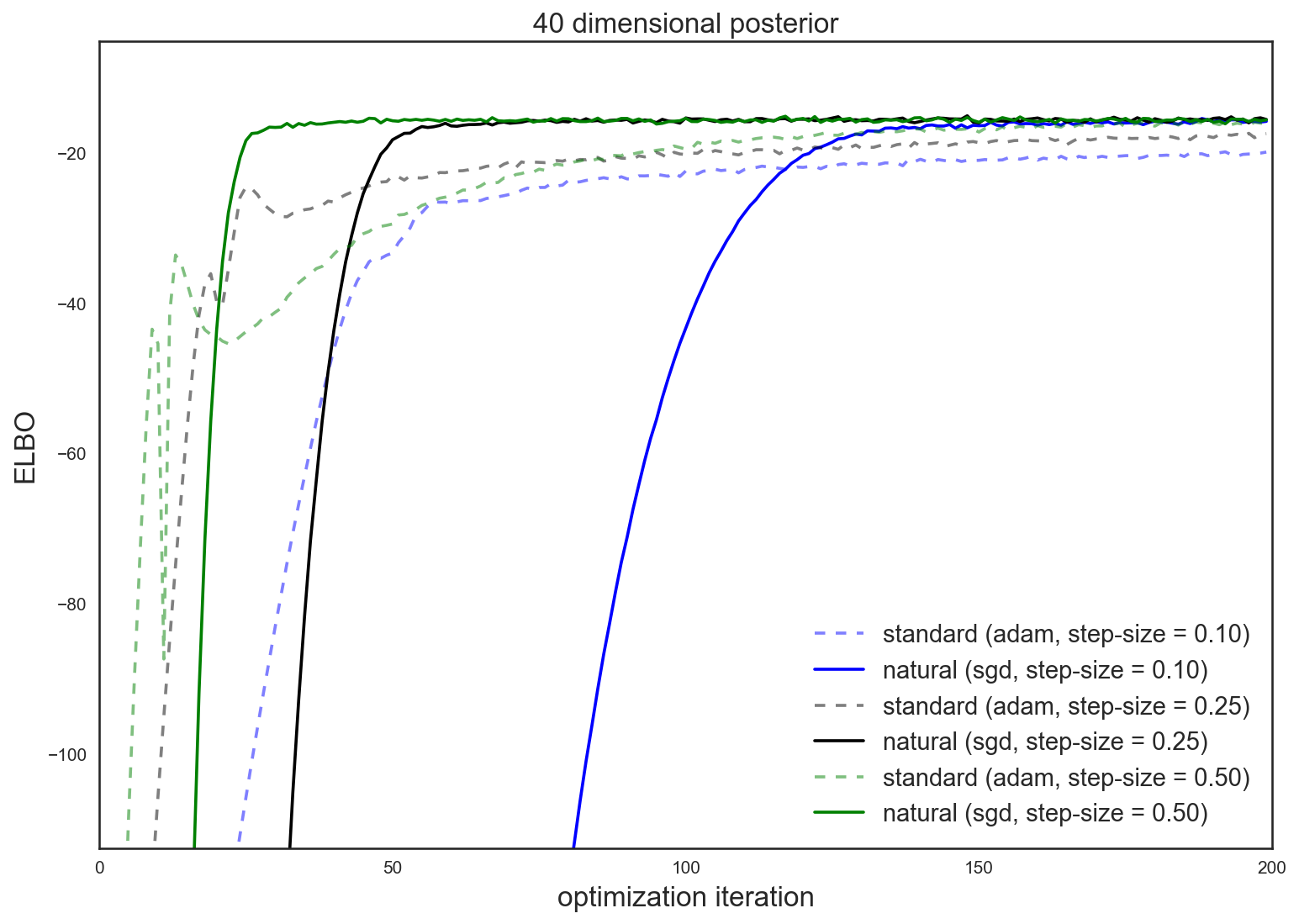
Natural Gradients and Stochastic Variational Inference
2 October 2016
Overview
My goal with this post is to build intuition about natural gradients for optimizing over spaces of probability distributions (e.g. for variational inference). I’ll examine a simple family of distributions (diagonal-covariance Gaussians) and try to see how natural gradients differ from standard gradients, and how they can make existing algorithms faster and more robust.
(expand) -
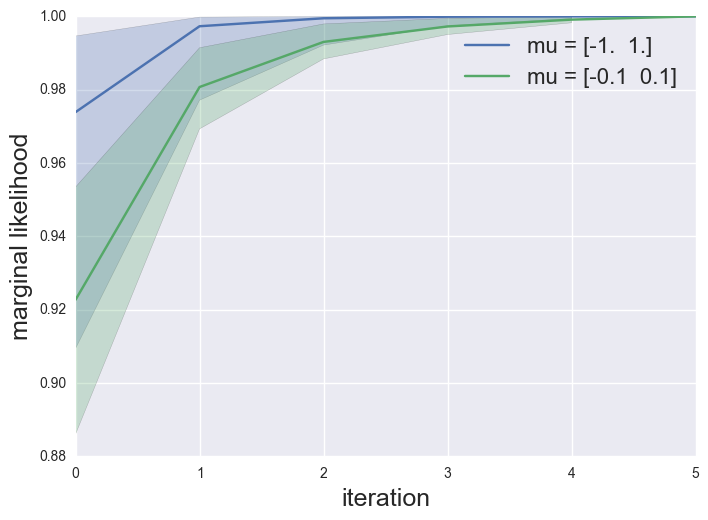
Expectation Maximization and Gradient Updates
15 October 2015
There are many ways to obtain maximum likelihood estimates for statistical models, and it’s not always clear which algorithm to choose (or why). There appears to be a natural divide between fixed-point iterative methods, such as Expectation Maximization (EM), and directly optimizing the marginal likelihood with gradient-based methods. One great reference that bridges this gap is the paper Optimization with EM and Expectation-Conjugate-Gradient by Salakhutdinov, Roweis and Ghahramani from ICML in 2003. The main takeaway of the paper is that an EM iteration can be viewed as a preconditioned gradient step on the marginal likelihood.
(expand) -
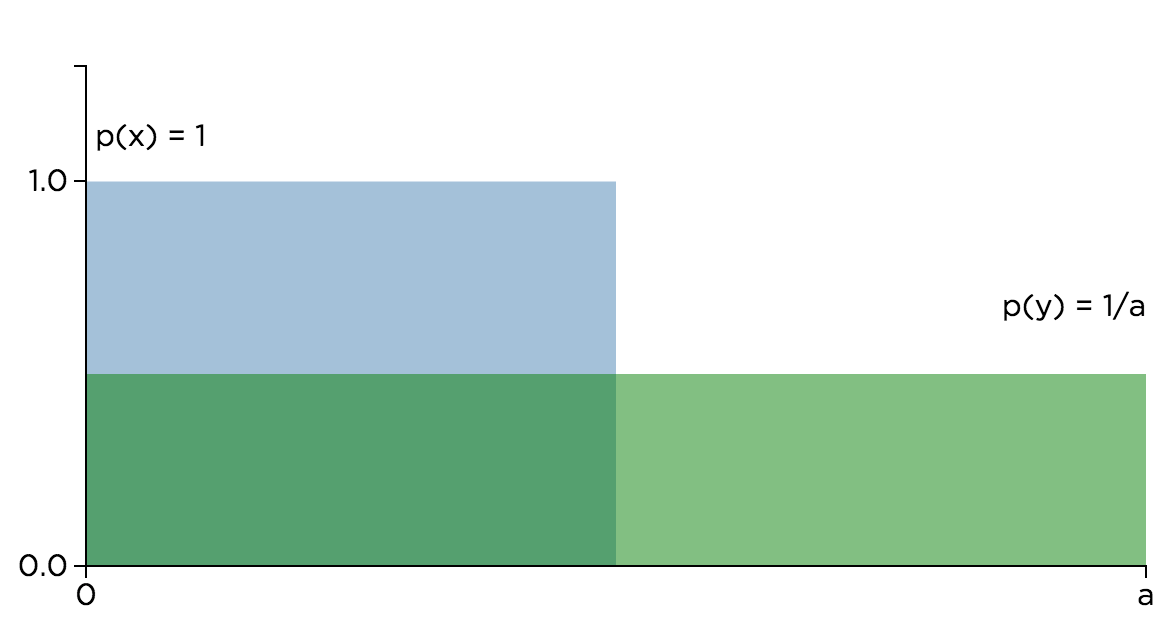
Trans-dimensional change of variables and the integral Jacobian
9 August 2015
I’ve been trying to solidify my understanding of manipulating random variables (RVs), particularly transforming easy-to-use RVs into more structurally interesting RVs. This note will go over the standard univariate change of variables method, and then expand on probability density functions for more complicated maps using the integral Jacobian.
(expand) -

Hello World!
5 August 2015
Hello, dear reader - welcome to my blog!
(expand)
My goal is to write about research ideas and concepts related to statistical machine learning to serve as a reference to my future self, and hopefully others will find it useful.