Andrew Miller

Monte Carlo Gradient Estimators and Variational Inference

19 Dec 2016

First, I’d like to say that I thoroughly enjoyed the the Advances in Approximate Bayesian Inference workshop at NIPS 2016 — great job Dustin Tran et al. An awesome poster (with a memorable name) from Geoffrey Roeder, Yuhuai Wu, and David Duvenaud probed an important, but typically undiscussed choice that practitioners have to make when doing black-box variational inference with the pathwise gradient estimators¹. This post describes the phenomenon that they point out. I will try to provide some additional intuition through wordy prose and a numerical experiment on a simple example.

We use variational inference (VI) to approximate a posterior distribution, \(p(z | x)\), with a tractable approximation, \(q_\lambda(z)\). To remain applicable to a general class of models, we often turn to Monte Carlo VI methods (e.g. black-box VI or autodiff VI), where we estimate certain expectations with respect to \(q_\lambda\) using samples.

Users of VI have a choice: which Monte Carlo estimator of the ELBO should we use? We typically write the ELBO objective in a few standard ways²

(i) KL form	\(\mathcal{L}_{KL}(\lambda) = \mathbb{E}_{q_\lambda}[\ln p(x \vert z)] - KL(q_\lambda \vert\vert p(z))\)
(ii) Entropy form	\(\mathcal{L}_{ent}(\lambda) = \mathbb{E}_{q_\lambda}[\ln p(x, z)] + H(q_\lambda)\)
(iii) Fully Monte Carlo (FMC) form	\(\mathcal{L}_{fmc}(\lambda) = \mathbb{E}_{q_\lambda}[\ln p(x, z) - \ln q_\lambda(z)]\)

where the functionals \(KL(\cdot || \cdot)\) and \(H(\cdot)\) are the Kullback-Leibler divergence and the entropy, respectively.

Because these expressions all involve an expectation, we cannot guarantee that \(\mathcal{L}_{(\cdot)}\) will be tractable for general \(p(x, z)\). We side-step this issue by approximating the objective (and its gradient) with samples from \(q_\lambda\); for instance, the entropy form approximation is computed

\[\begin{align} \hat{\mathcal{L}}_{ent}(\lambda) = \frac{1}{L} \sum_{\ell} \ln p(x, z^{(\ell)}) + H(q_\lambda) \, , \quad z^{(\ell)} \sim q_\lambda \end{align}\]

and the fully Monte Carlo form is computed

\[\begin{align} \hat{\mathcal{L}}_{fmc}(\lambda) &= \frac{1}{L} \sum_{\ell} \ln p(x, z^{(\ell)}) - \ln q_\lambda(z^{(\ell)}) \, , \quad z^{(\ell)} \sim q_\lambda \end{align}\]

Both estimators, \(\hat{\mathcal{L}}_{ent}\) and \(\hat{\mathcal{L}}_{fmc}\), are random variables, seeded by the randomness originating from \(q_\lambda\); both estimators will have some variance (they are unbiased, so they will have the same mean).

Notice the subtle difference between the two — the entropy estimator computes the entropy in closed form (which is possible in the case of tractable \(q\) distributions), whereas the full Monte Carlo estimator computes that term via Monte Carlo — recall that \(H(q_\lambda) \triangleq - \mathbb{E}_{q_\lambda}[\ln q_\lambda(z)]\).

We might expect the KL or entropy forms, where a part of the expectation is analytically integrated out, to have lower variance when estimating with Monte Carlo samples — and that intuition is correct sometimes, but not all the time. When \(q_\lambda\) is flexible enough, and close to \(p(z | x)\), then the randomness in \(\hat{\mathcal{L}}_{fmc}\) is “canceled out” in each term in the sum

\[\begin{align} &\ln p(x, z^{(\ell)}) - \ln q_\lambda(z^{(\ell)}) \\ &\quad= \ln p(z^{(\ell)} | x) p(x) - \ln q_\lambda(z^{(\ell)}) \\ &\quad= \underbrace{\ln p(z^{(\ell)} | x) - \ln q_{\lambda}(z^{(\ell)})}_{\text{approx. } 0} + \underbrace{\ln p(x)}_{\text{const.}} \end{align}\]

so when \(q_\lambda(z) = p(z | x)\), the full Monte Carlo estimator has zero variance. In fact, we see that the KL and Entropy estimators will always have some irreducible variance from estimating the data term, even when we’ve accomplished our goal of \(q_\lambda(z) = p(z | x)\). However, when \(q_\lambda(z) \neq p(z|x)\), the FMC estimator can have much, much larger variance than the Entropy estimator.

Gradient Estimators

When optimizing, we care more about the variance of the gradient of the ELBO than the value of the ELBO itself. The pathwise gradient estimator uses the reparameterization trick to turn a Monte Carlo ELBO estimator into a Monte Carlo ELBO gradient estimator, \(\nabla_\lambda \hat{\mathcal{L}}_{(\cdot)}\), which we then use in a gradient-based optimization procedure. The variance in the gradient estimator will profoundly affect the (practical) speed of convergence of optimization.

The natural question becomes, what is the variance of the gradient estimators derived from the above ELBO forms? Roeder et al. look at the variance of the pathwise gradient estimator as applied to the fully Monte Carlo form. For a single sample \(z_\lambda = f(\epsilon, \lambda)\)³ the pathwise gradient of the fully Monte Carlo estimator can be written

\[\begin{align} \mathcal{L}_{fmc} &= \ln p(x, z_\lambda) - \ln q(z_\lambda, \lambda) \\ \nabla_\lambda \mathcal{L}_{fmc} &= \frac{\partial}{\partial \lambda} \ln p(x, z_\lambda) - \frac{\partial}{\partial \lambda} \ln q(z_\lambda; \lambda) \end{align}\]

One thing tripped me up at first: the second term is a function of \(\lambda\) through two different arguments, \(z_\lambda\) and \(\lambda\) itself. This allows us to decompose the gradient into two components: (i) variation due to dependence through \(z_\lambda\) and (ii) dependence on \(\lambda\) directly through the probability density function \(q(z; \lambda)\). In fact, we can view the entire gradient through the lens of this decomposition

\[\begin{align} \nabla_\lambda \mathcal{L}_{fmc} &= \underbrace{\frac{\partial \ln p(x, z_\lambda)}{\partial z_\lambda} \frac{\partial z_\lambda}{\partial \lambda} - \frac{\partial \ln q(z_\lambda; \lambda)}{\partial z_\lambda} \frac{\partial z_\lambda}{\partial \lambda}}_{\text{pathwise}} - \underbrace{\frac{\partial \ln q(z; \lambda)}{\partial \lambda} \Big|_{z=z_\lambda}}_{\text{score fun.}} \end{align}\]

where the pathwise term accounts for variation via \(z_\lambda\), and the score function term accounts for variation through the pdf of \(q(z; \lambda)\), which varies as a function of \(\lambda\) even when the first argument, \(z\), is held fixed.

This expression makes clear that the data term, \(\ln p(x, z_\lambda)\), only varies as a function of \(\lambda\) through \(z_\lambda\). So when we have a nearly perfect approximation, \(\ln q(z; \lambda)\), their gradients with respect to \(z\) are close, i.e.

\[\begin{align} \frac{\partial \ln p(x, z)}{\partial z} \approx \frac{\partial \ln q(z; \lambda)}{\partial z} \end{align}\]

When our approximation is almost there the pathwise component of the gradient is always close to zero for a sample \(z^{(\ell)}\). In this regime, the source of variance of the gradient estimator is the score function term

\[\begin{align} \frac{\partial \ln q(z; \lambda)}{\partial \lambda} \Big|_{z=z_\lambda} \, \quad z_\lambda \sim q_\lambda \end{align}\]

The score function has expectation zero — so we can simply remove (or scale) it. The question becomes: when should we reduce or remove the score function component of the pathwise gradient estimator?⁴

Numerical Example

To get a sense of the variance of these gradient estimators, I used a \(D=25\) dimensional Gaussian (with non-trival covariance) as the target distribution, and a \(q\) in the same Gaussian family. Optimizing the ELBO with the pathwise gradient of the entropy estimator (note the noisy path near convergence) I measured the variance of each gradient component, \(\mathbb{V}( \nabla_{\lambda_i} \mathcal{L}(\lambda) )\), at each step of the optimization (for each the ~100 \(\lambda\) parameters).

The animation below compares the standard deviation (not variance) of three estimators

• pathwise entropy
• pathwise full monte carlo
• pathwise full monte carlo, removing the score function term (from Roeder et al.)

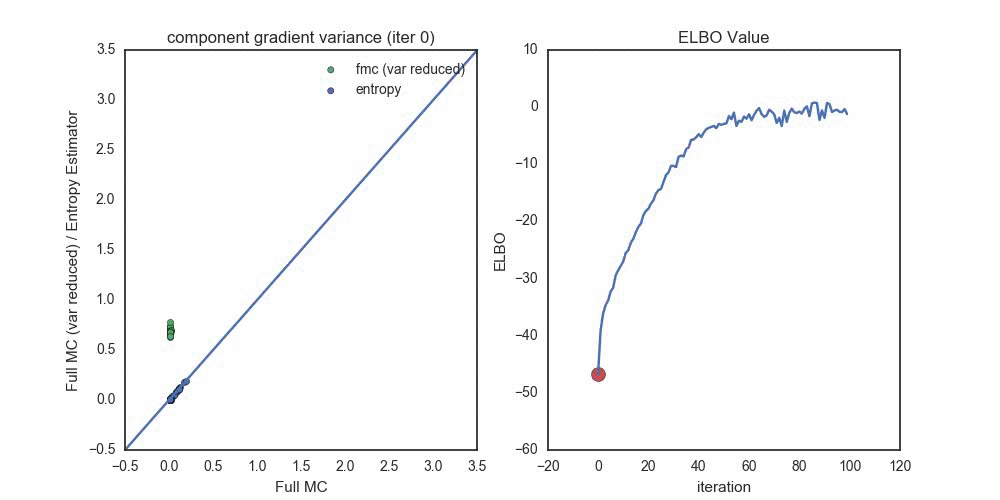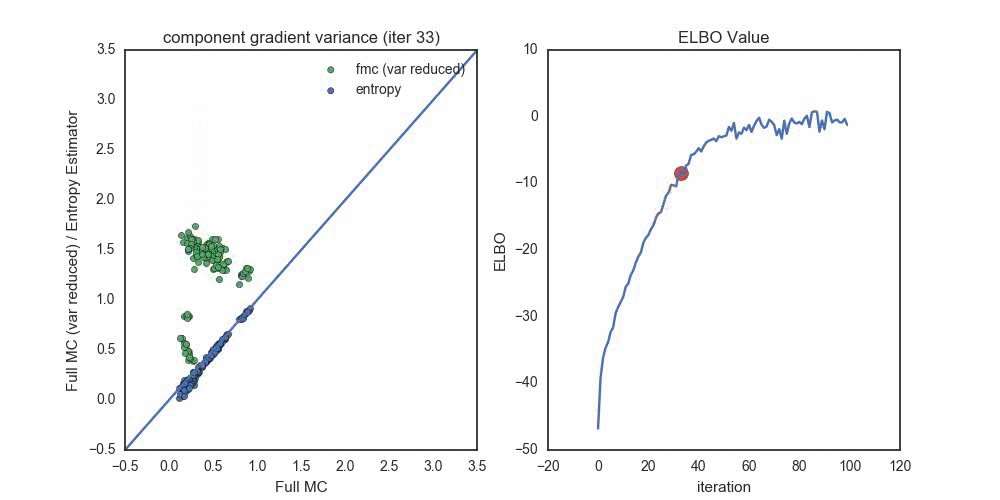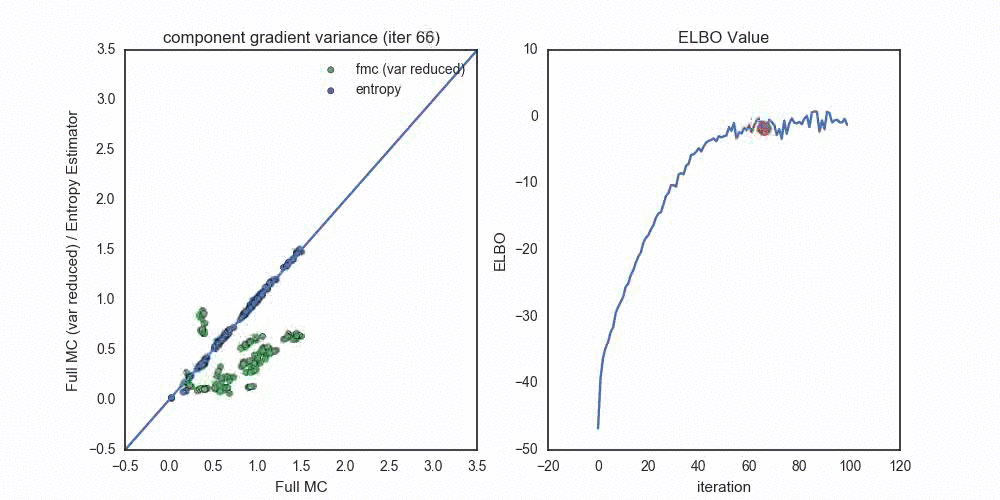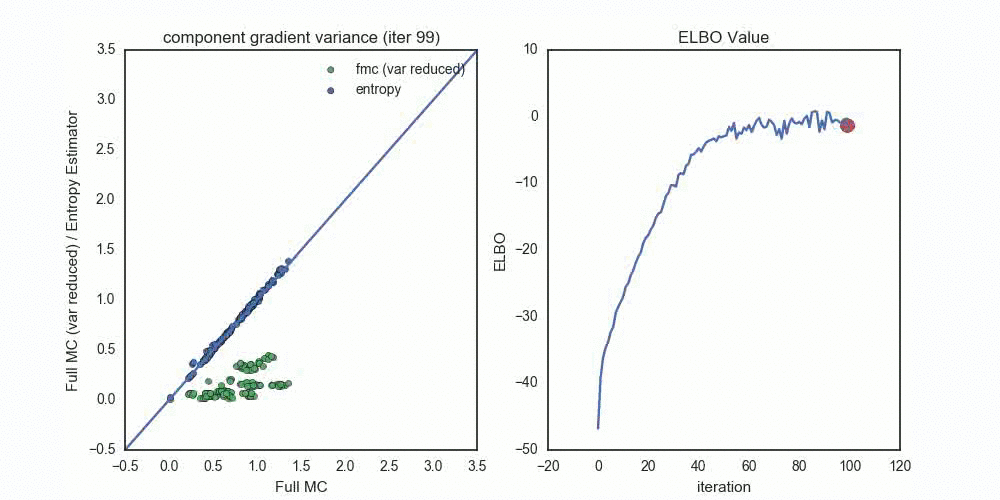
Each dot compares the standard deviation of a gradient component, where

• Blue dots compare the entropy estimator (y-axis) to the full Monte Carlo estimator (x-axis).
• Green dots compare the full Monte Carlo without the score function term (y-axis) to the full Monte Carlo estimator (x-axis).

Notice the progression — when the optimization starts out with \(q_\lambda\) very far from \(p(z | x)\), the Entropy estimator provides (by far) the lowest variance estimates (across all components). As we reach convergence, the variance reduced FMC estimates shrink toward zero — once we’re within about 2-3 nats of the true distribution. Had I used the variance reduced FMC estimator at this point in the optimization, we probably would see a much faster variance decrease in the green dots.

In this scenario, the pathwise entropy estimator dominates the pathwise FMC estimator — we should never choose the FMC for gradients, unless we’re variance-reducing them near the end of the optimization procedure.

Another interesting thing to note here is that the entropy estimator and full Monte Carlo estimator settle to essentially identitical component variances. This makes sense when \(q_\lambda\) and \(p(z|x)\) are close — the variance of the score function gradient component will be equal to the variance of the pathwise component that relies on \(\ln p(x,z)\).

This numerical experiment suggests finding some tradeoff that gradually removes the score function component — that way the optimization procedure can enjoy the early benefits of the entropy estimator with the late benefits of the reduced variance. I’m also curious how the variance of pathwise estimators affects natural gradients, and consequently their convergence properties.

Looking forward to the full paper!

Hasta luego, Barcelona …

---